- Importance Of Serial Dilution Technique
- Importance Of Serial Dilution In Serology
- Serial Dilution
- Importance Of Serial Dilution In Pharmacy
Serial dilution, also called limiting dilution series, is a standard laboratory procedure employed to collect the appropriate data in order to accomplish this estimation. Our designs for this experiment must maximize the probability that useful data will be obtained since these experiments are costly, labor intensive, and time consuming. Serial dilution is one of the core foundational practices of homeopathy, with 'succussion', or shaking, occurring between each dilution.In homeopathy, serial dilutions (called potentisation) are often taken so far that by the time the last dilution is completed, no molecules of the original substance are likely to remain.
Abstract
We describe statistical plans for a serial dilution series designed to detect and estimate the number of viral particles in a solution. The design addresses a problem when a very limited number of aliquots are available for proliferation. A gamma prior distribution on the number of viral particles allows us to describe the marginal probability distribution of all experimental outcomes. We examine a design that minimizes the expected reciprocal information and compare this with the maximum entropy design. We argue that the maximum entropy design is more useful from the point of view of the laboratory technician. The problem and design are motivated by our study of the viability of human immunodeficiency virus in syringes and other equipment that might mediate blood-borne viral transmission.
1. Introduction
We want to design a method to estimate a small number of viral particles as a part of our studies of human immunodeficiency virus (HIV) survival in injection equipment. Ultimately we want to make public health recommendations of relevance to HIV prevention programs, such as syringe exchange and harm reduction. We want to develop accurate advice to provide to intravenous drug users on how to effectively clean syringes using clean water, bleach, other disinfectants, or other liquids. To do so, we first need a method for estimating the effectiveness of such strategies. This involves estimating the number of viable HIV virions remaining in a used syringe.
Serial dilution, also called limiting dilution series, is a standard laboratory procedure employed to collect the appropriate data in order to accomplish this estimation. Our designs for this experiment must maximize the probability that useful data will be obtained since these experiments are costly, labor intensive, and time consuming. Estimates are sufficient for our needs if they identify the number of replicating viral particles up to an order of magnitude, or perhaps, indicate whether or not the number of these particles falls in a wide interval of interest as described below. The technician also seeks feedback on the quality of the experimental method. We will argue that traditional statistical concerns, such as bias and mean-squared error, are sometimes of secondary importance to the laboratory technician in this design consideration. Further, moments of the maximum likelihood estimate are undefined.
In our laboratory a used syringe is rinsed out and its contents are then successively diluted in several stages. Each subsequent fractional dilution or aliquot is inoculated with target CD4+ cells in order to detect the presence of at least one replicating viral particle. This expensive and time-consuming fermentation step limits the number of aliquots available to us. The titer of virus is defined as the number of viable virus particles originally present in the sample being tested and is usually expressed in terms of concentration of the original solution but can also be expressed as the estimated number of particles. The laboratory procedure does not allow us to obtain the results of one dilution step before proceeding with the next. All aliquots must be diluted and cultured simultaneously.
The replication of HIV is monitored by determining the amount of viral products generated in culture, usually the quantification of the amount of the viral protein produced during viral replication [] using an enzyme immunoassay. This technique employs enzyme-linked antibodies that bind specific viral proteins and produce, enzymatically, a colored product that is quantified spectroscopically. The extent of viral replication is based on a change in the light absorption following 2–3 weeks of culture.
The design for the dilutions and their replicates is planned in such a manner as to allow identification of the titer, and subsequently, estimation of the initial number of viable particles N. Many published plans are designed for detecting very large numbers of viable particles, often measured in the millions. In contrast, our range of interest for N, described next, is limited to a few hundred at most. Similarly, published designs often call for many dozens of replicates of many diluted fractions of the original solution ([2], for example) consisting of hundreds of total aliquots. Our budget, on the other hand, limits us to 10 aliquots at most.
We are looking for an estimate of a relatively small number of viable viral particles, in the range of 4–400 [, ]. A value of 4 viable virions is commonly accepted as the lowest limit of detection in these studies. We set an upper limit at 400 because the small volume of residual blood in syringes is unlikely to contain more virus. These limits motivate our choice of parameters for the prior distribution on N described in Section 2 at (5), below.
Serial dilution is a long established laboratory procedure. Standard statistical methods for the analysis of the data include maximum likelihood estimation for the number of viral particles N. These methods are reviewed in [] and outlined in Section 2. Recent statistical methods for estimating N include the development of mixed effect models for these experiments by Zackin et al. [6], Higgins et al. [], and Bloch and Chavance []. Ridout [9], and Wang and Basu [] compare confidence interval methods. Chick [2], Mehrabi and Matthews [11], Gelman et al. [], and Stallard et al. [13] describe Bayesian analyses of these data using normal and log-normal prior distributions on N. We will assume a gamma prior distribution. Numerical integration permits the use of other prior distributions on N. The Appendix illustrates some closed-form results when we assume a gamma prior distribution.
Other recent statistical developments include a jackknife estimate of the bias and variance in [14]. Bayesian design methods for this problem and the closely related topic of logistic regression have been developed in [15–17] and are reviewed in [18]. A design method in [11] based on the expected reciprocal information is described in Section 2 and compared with our proposed maximum entropy methods in Section 4.
Section 2 introduces the notation and describes a statistical analysis of these data following a traditional likelihood approach. Section 3 motivates a maximum entropy design from the point of view of the laboratory technician performing the experiment. Section 4 contains specific design recommendations in the context of our present setting of the syringe hygiene and harm reduction program. Section 4 makes recommendations for more general settings including other numbers of aliquots and sensitivity to the prior distribution. The mathematical details of the marginal distribution of the observations are described in the Appendix.
2. Notation and methods
A solution contains N live viral particles and our object is to design a study to draw statistical inference on this value. The approach taken in the laboratory is to dilute this solution several times and determine the presence of viral replication in culture in each of the fractional wells or aliquots. Some fractions might also be replicated as part of the statistical design. Binary-valued data result from identifying those aliquots containing at least one viable virus particle at the time of the dilution. These binary values are determined by whether or not the diluted solution yields a colored product after enzyme immunoassay. From this binomial distributed data, we must infer the value of N. The limited number of aliquots available to us and the motivating problem of harm reduction suggests that we are willing to accept an estimate of N accurate up to only an order of magnitude. The actual value of N is as important as knowing whether or not it falls in the interval 4–400. In Section 3 we explain how a design can also be used to provide important feedback on the quality and care involved in the conduct of the laboratory procedure.
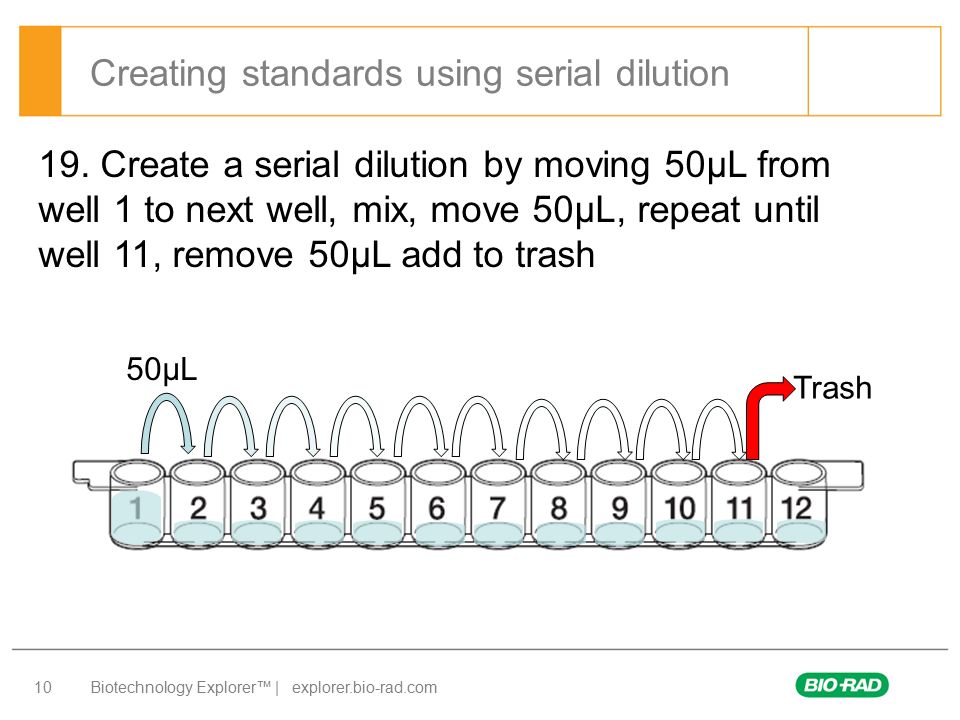
To introduce some notation, suppose the initial sample is diluted in k stages (k=1,2,…). At the ith stage (i=1,…,k), the solution is diluted at the (incremental) rate of di:1(di>1) from the previous stage. (We take the zeroth stage to be the initial sample.) The ith dilution is replicated ni times for ni=1,2….
In our prototypical study, for example, we plan onk=5 stages of dilution. Each dilution is replicated (i.e. all ni=2) for a total of σni=10 aliquots to be cultured. This figure of 10 is the maximum amount that time, labor, and money permit us. This is approximately the number of aliquots that we will be concerned with but our results also hold more generally. Each stage of our prototype represents concentration of the previous so d1=…=d5=3.84. Laboratory pipettes are continuously adjustable so a fractional dilution rate does not pose a problem. The derivation of this specific rate of dilution will be explained later in this section. It is also possible to design experiments where we vary the dilution rate within the same aliquot series but we will not examine these because of the introduction of another chance of laboratory error. That is, we will only consider a constant value of di=d in the remainder of this work.
The most likely outcomes of the prototype design are given in Table I. Only those outcomes with a marginal probability greater than 0.005 are included. An expression for the posterior mean of N is given in the Appendix. A variety of designs, each with 10 aliquots, is given in Table II. Designs with other numbers of aliquots are also possible and are described in Section 4.
Table I
The most likely outcomes of the prototype design with k=5 stages of d=3.84:1 serial dilutions, replicated (all ni=2) at each stage.
| Outcome y | Marginal Pr[Y=y] | Estimated | Posterior Mean | |||||
|---|---|---|---|---|---|---|---|---|
| y1 | y2 | y3 | y4 | y5 | ||||
| 0 | 0 | 0 | 0 | 0 | 0.0073 | 0.00 | 0.00 | 1.39 |
| 1 | 0 | 0 | 0 | 0 | 0.0102 | 1.06 | 1.04 | 3.45 |
| 2 | 0 | 0 | 0 | 0 | 0.0175 | 3.22 | 2.25 | 8.72 |
| 1 | 1 | 0 | 0 | 0 | 0.0060 | 2.30 | 1.74 | 5.54 |
| 2 | 1 | 0 | 0 | 0 | 0.0367 | 6.26 | 4.14 | 15.49 |
| 2 | 2 | 0 | 0 | 0 | 0.0589 | 13.88 | 9.30 | 32.56 |
| 2 | 0 | 1 | 0 | 0 | 0.0061 | 5.56 | 3.67 | 13.05 |
| 2 | 1 | 1 | 0 | 0 | 0.0249 | 10.53 | 7.10 | 22.80 |
| 2 | 2 | 1 | 0 | 0 | 0.1106 | 26.29 | 16.94 | 53.72 |
| 2 | 1 | 2 | 0 | 0 | 0.0068 | 16.86 | 11.13 | 32.37 |
| 2 | 2 | 2 | 0 | 0 | 0.1248 | 56.51 | 37.28 | 97.48 |
| 2 | 1 | 0 | 1 | 0 | 0.0055 | 10.07 | 6.79 | 21.68 |
| 2 | 2 | 0 | 1 | 0 | 0.0197 | 23.32 | 15.07 | 46.82 |
| 2 | 1 | 1 | 1 | 0 | 0.0056 | 15.89 | 10.54 | 30.44 |
| 2 | 2 | 1 | 1 | 0 | 0.0655 | 43.16 | 28.29 | 76.25 |
| 2 | 2 | 2 | 1 | 0 | 0.1575 | 107.39 | 70.07 | 144.73 |
| 2 | 2 | 1 | 2 | 0 | 0.0147 | 68.35 | 44.93 | 104.73 |
| 2 | 2 | 2 | 2 | 0 | 0.0875 | 244.39 | 167.77 | 216.32 |
| 2 | 2 | 1 | 0 | 1 | 0.0149 | 41.27 | 27.00 | 73.24 |
| 2 | 2 | 2 | 0 | 1 | 0.0317 | 94.53 | 61.62 | 133.49 |
| 2 | 2 | 1 | 1 | 1 | 0.0127 | 64.31 | 42.34 | 99.83 |
| 2 | 2 | 2 | 1 | 1 | 0.0615 | 178.90 | 120.67 | 193.25 |
| 2 | 2 | 2 | 2 | 1 | 0.0540 | 510.82 | 369.74 | 285.79 |
| 2 | 2 | 2 | 1 | 2 | 0.0083 | 288.68 | 199.08 | 250.15 |
| 2 | 2 | 2 | 2 | 2 | 0.0116 | — | — | 369.18 |
| Total: | 0.9608 | |||||||
This dilution rate minimizes the expected reciprocal information. Of 35=243 possible outcomes, only those with a marginal probability Pr[Y]≥0.005 given by (6) are included here. The gamma prior distribution for N is described at (5) and places 95 per cent probability on the interval 4–400.
Table II
Several selected designs obtained from a complete enumeration of all 512 designs with 10 aliquots
| Stages k | Allocation n | Dilution rates | Maximum entropy | E{1/I(dI)}×10−3 | |
|---|---|---|---|---|---|
| dE | dI | ||||
| 2 | ( 1 9 )b | 11.50 | 22.44 | 4.93 | 5.37 |
| 2 | ( 2 8 ) | 12.13 | 25.40 | 4.95 | 6.04 |
| 3 | ( 1 8 1 ) | 9.47 | 22.46 | 5.28 | 5.51 |
| 3 | ( 1 7 2 ) | 8.41 | 22.66 | 5.49 | 6.14 |
| 3 | ( 2 7 1 ) | 9.86 | 25.25 | 5.24 | 6.29 |
| 5 | ( 2 2 2 2 2 )a | 3.55 | 3.84 | 5.88 | 11.84 |
| 6 | ( 1 1 2 2 2 2 ) | 3.00* | 3.00* | 6.59 | 9.59 |
| 7 | ( 1 1 2 2 2 1 1 ) | 3.00* | 3.00* | 6.53 | 9.36 |
| 7 | ( 1 1 1 2 2 2 1 ) | 3.00* | 3.00* | 6.56 | 9.16 |
| 9 | ( 1 1 1 1 1 1 1 1 2 ) | 2.01 | 2.00* | 6.74 | 12.87 |
| 10 | ( 1 1 1 1 1 1 1 1 1 1 )c | 2.00* | 2.00* | 6.84 | 11.86 |
Design a is the prototype, b is the minimum expected reciprocal information and c is the maximum entropy design. Details of these three designs appear in Tables I, III, and andIV,IV, respectively.
Following a period of culture, each of the 10 aliquots result in Bernoulli distributed indications of whether or not each of the fractional aliquots contained at least one replicating viral particle at the time of the dilution. The statistical problem, described here, is to design the dilution experiment in terms of the parameters: k stages, dilution rate d, and replicates n={ni} for a specified number of aliquots Σni.
The probability that a given aliquot at the ith dilution will result in detection of at least one replicating viral particle is
where
is the aliquot fraction of the original solution obtained from the used syringe.
In order for there to be sufficient amount of solution to perform the series we must also have
An important assumption made here is that λi also represents the fraction of the original N viruses and these are uniformly and independently distributed throughout the medium. Also note that the volume of the original solution is neither needed in the statistical analysis nor it is used in these expressions. In our laboratory practice, for example, the used syringe is rinsed out and this solvent is diluted to a convenient working volume. Similarly, many studies express N in terms of virions per unit volume, as opposed to our approach of treating N as an absolute number. The approximation pi ≈ 1−exp{−Nλi} is often used at (1) when N is known to be very large and λi is small but we will not use this approximation.
Let Yi denote the independent, binomially distributed number of aliquots that test positive following culture of the ith stage of the dilution. The joint likelihood of the counts Y ={Yi} given the initial number of viral particles N is
for y ={yi} and yi=0,1,…,ni.
The estimate of N is that value maximizing this likelihood. The expected information (given below) is used to approximate the variance of . The exact distribution of is discrete and is illustrated in Tables I, III, and andIVIV for different designs. The estimate is not restricted to integer values.
Table III
This design with k=2 stages, n=(1,9), and dI=22.44 minimizes the expected reciprocal information over all designs with 10 aliquots.
| Outcome y | Marginal Pr[Y=y] | Estimated | Posterior mean | ||
|---|---|---|---|---|---|
| y1 | y2 | ||||
| 0 | 0 | 0.1060 | 0.00 | 0.00 | 15.23 |
| 0 | 1 | 0.0297 | 0.32 | 0.41 | 29.28 |
| 1 | 0 | 0.2080 | 1.38 | 2.47 | 53.05 |
| 1 | 1 | 0.2152 | 24.84 | 24.85 | 86.23 |
| 1 | 2 | 0.1673 | 52.99 | 37.57 | 124.99 |
| 1 | 3 | 0.1150 | 85.49 | 49.70 | 169.29 |
| 1 | 4 | 0.0725 | 123.94 | 62.87 | 219.24 |
| 1 | 5 | 0.0419 | 170.99 | 78.58 | 275.42 |
| 1 | 6 | 0.0217 | 231.64 | 99.40 | 338.99 |
| 1 | 7 | 0.0096 | 317.14 | 131.49 | 411.87 |
| Total: | 0.9941 | ||||
Only those outcomes with a marginal probability greater than 0.005 are listed.
Table IV
The design with k=10 stages and all ni=1 maximizes the entropy over all designs with 10 aliquots.
| Outcome y | Marginal Pr[Y=y] | Estimated | Posterior mean | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y1 | y2 | Y3 | y4 | y5 | y6 | y7 | y8 | y9 | y10 | ||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0065 | 1.18 | 1.12 | 2.76 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0122 | 3.30 | 2.39 | 6.33 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0238 | 7.27 | 4.97 | 13.12 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0070 | 6.26 | 4.30 | 10.43 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0450 | 15.26 | 10.18 | 25.74 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0.0138 | 13.24 | 8.86 | 20.97 |
| 1 | 1 | 1 | 1 | i | 0 | 0 | 0 | 0 | 0 | 0.0772 | 31.44 | 20.78 | 47.93 |
| a1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0.0057 | 12.55 | 8.41 | 19.61 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0.0250 | 27.31 | 18.07 | 40.14 |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0.0058 | 21.68 | 14.38 | 30.36 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0.1117 | 64.58 | 42.73 | 83.61 |
| a1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0.0105 | 25.90 | 17.15 | 37.76 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0.0386 | 55.99 | 37.02 | 72.53 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0.0099 | 44.48 | 29.39 | 57.22 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0.1242 | 134.30 | 89.91 | 134.61 |
| a1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0.0165 | 53.06 | 35.07 | 68.87 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0.0464 | 115.61 | 77.13 | 121.58 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0.0133 | 91.28 | 60.64 | 101.16 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0.0969 | 290.00 | 200.27 | 199.13 |
| b1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0.0077 | 51.80 | 34.24 | 67.34 |
| a1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0.0204 | 109.33 | 72.86 | 116.84 |
| c1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0.0060 | 87.98 | 58.42 | 98.24 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0.0392 | 245.07 | 167.69 | 186.70 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0.0129 | 190.01 | 128.59 | 164.62 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0.0493 | 699.26 | 526.77 | 273.22 |
| b1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0.0096 | 106.66 | 71.05 | 114.79 |
| a1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0.0178 | 230.58 | 157.31 | 181.72 |
| c1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0.0059 | 182.78 | 123.52 | 161.04 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0.0214 | 557.68 | 407.45 | 263.30 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0.0080 | 411.56 | 291.53 | 244.09 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.0156 | — | — | 353.31 |
| Total: | 0.9043 | ||||||||||||
The optimal dilution rate dE=2 is achieved at the boundary given by (3). Only events with a marginal probability greater than 0.005 are included. Outcomes labeled a skip two levels, b skip three levels; and c exhibit staggered skips.
The event {Y =n} means that all aliquots at all dilutions and replications grew following viral culture indicating the presence of at least one viral particle. When Y =n, the binomial likelihood in (4) is an always-increasing function of N. The value of is then undefined when Y =n. The probability of {Y =n} at (4) is non-zero, so the moments of are not defined. Lee and Whitmore [] describe a truncated estimator of N that has all defined moments. In this work we will assume a gamma prior distribution on N. The posterior moments of N are all finite, even when is not defined. A formal Bayesian analysis might use the 95 per cent maximum credibility region of the posterior distribution to create a confidence interval of the estimate.
The standard error of is undefined in the formal mathematical definition. We can still estimate the standard error of for the purpose of constructing confidence intervals through the expected information. The expected information for N in (4) is
The estimated standard error of given in Tables I, III, and andIVIV is calculated as:
When Y =n the estimate is undefined as is this estimated standard error.
In designing the study we found that it is mathematically convenient to describe our a priori knowledge of N in terms of a gamma random variable. The gamma prior distribution will not be employed in a formal Bayesian analysis but rather will be used as a convenient way of expressing our range of interest for this parameter. In the absence of better knowledge of the true value of N, this prior distribution allows us to find a useful expression for the marginal probability Pr[Y]. In References [2, 11, ], as well as in the present work, it is suggested that little is lost by approximating the discrete distribution of N by a continuous-valued prior distribution.
The gamma density function describing the prior distribution of N is denoted
for N,α,σ all non-negative with expected value α/σ.
Values of α=1.1168 and σ=9.8255×10−3 correspond to the gamma prior distribution (5) on N with 95 per cent coverage of the interval 4–400 and 2.5 per cent outside each end of this range. These parameter values are used in our prototype design of Table I and in our search over all possible designs with 10 aliquots in Table II. Optimal designs using this prior distribution and 10 aliquots are illustrated in Tables III and andIV.IV. The sensitivity for other parameter values of the gamma prior distribution and different numbers of aliquots are summarized in Tables V and andVIVI.
Table V
Minimum expected reciprocal information designs for small numbers of aliquots obtained by enumerating all possible designs.
| Aliquots | Coverage | Allocation n | Dilution rate dI | Minimum E(1/I)×10−3 |
|---|---|---|---|---|
| 4 | 0.999 | 1 3 | 34.76 | 7.42 |
| 0.99 | 1 3 | 46.43 | 10.12 | |
| 0.95 | 1 3 | 69.44 | 16.12 | |
| 0.90 | 1 3 | 93.83 | 23.45 | |
| 0.75 | 1 3 | 147.64 | 71.04 | |
| 5 | 0.999 | 1 4 | 25.80 | 5.57 |
| 0.99 | 1 4 | 34.56 | 7.59 | |
| 0.95 | 1 4 | 51.82 | 12.09 | |
| 0.90 | 1 4 | 70.12 | 17.56 | |
| 0.75 | 1 4 | 144.56 | 46.92 | |
| 6 | 0.999 | 1 5 | 20.42 | 4.45 |
| 0.99 | 1 5 | 27.44 | 6.07 | |
| 0.95 | 1 5 | 41.25 | 9.67 | |
| 0.90 | 1 5 | 55.89 | 14.07 | |
| 0.75 | 1 5 | 115.44 | 37.54 | |
| 8 | 0.999 | 1 7 | 14.26 | 3.18 |
| 0.99 | 1 7 | 19.28 | 4.34 | |
| 0.95 | 1 7 | 29.16 | 6.91 | |
| 0.90 | 1 7 | 39.62 | 10.05 | |
| 0.75 | 1 7 | 82.17 | 26.81 | |
| 10 | 0.999 | 1 9 | 10.83 | 2.47 |
| 0.99 | 1 9 | 14.75 | 3.37 | |
| 0.95 | 1 9 | 22.44 | 5.37 | |
| 0.90 | 1 9 | 30.58 | 7.82 | |
| 0.75 | 1 9 | 63.68 | 20.86 | |
| 12 | 0.999 | 1 10 1 | 11.00* | 2.05 |
| 0.99 | 1 11 | 11.85 | 2.76 | |
| 0.95 | 1 11 | 18.16 | 4.40 | |
| 0.90 | 1 11 | 24.83 | 6.39 | |
| 0.75 | 1 11 | 51.91 | 17.06 |
The gamma prior distribution on the number of virions places the specified coverage on the interval 4–400.


Table VI
Maximum entropy designs for small numbers of aliquots obtained by enumerating all possible designs.
| Aliquots | Coverage | Allocation n | Dilution rate dE | Maximum entropy |
|---|---|---|---|---|
| 4 | 0.999 | 4 | 114.09 | 3.11 |
| 0.99 | 4 | 114.26 | 3.18 | |
| 0.95 | 1 2 1 | 8.26 | 3.23 | |
| 0.90 | 1 2 1 | 8.13 | 3.33 | |
| 0.75 | 1 1 1 1 | 4.72 | 3.54 | |
| 5 | 0.999 | 1 1 2 1 | 4.68 | 3.55 |
| 0.99 | 1 1 2 1 | 4.68 | 3.71 | |
| 0.95 | 1 1 2 1 | 4.71 | 3.92 | |
| 0.90 | 1 1 2 1 | 4.75 | 4.03 | |
| 0.75 | 1 1 1 1 1 | 3.60 | 4.17 | |
| 6 | 0.999 | 1 1 1 2 1 | 3.42 | 4.13 |
| 0.99 | 1 1 1 2 1 | 3.42 | 4.31 | |
| 0.95 | 1 1 1 2 1 | 3.45 | 4.54 | |
| 0.90 | 1 1 1 2 1 | 3.48 | 4.66 | |
| 0.75 | 1 1 1 1 1 1 | 2.98 | 4.78 | |
| 8 | 0.999 | 1 1 1 2 2 1 | 3.00* | 5.36 |
| 0.99 | 1 1 1 2 2 1 | 3.00* | 5.54 | |
| 0.95 | 1 1 1 2 2 1 | 3.00* | 5.75 | |
| 0.90 | 1 1 1 2 2 1 | 3.00* | 5.85 | |
| 0.75 | 1 1 1 1 1 1 1 1 | 2.32 | 5.96 | |
| 10 | 0.999 | 1 1 1 1 1 1 1 1 1 1 | 2.00* | 6.30 |
| 0.99 | 1 1 1 1 1 1 1 1 1 1 | 2.00* | 6.55 | |
| 0.95 | 1 1 1 1 1 1 1 1 1 1 | 2.00* | 6.84 | |
| 0.90 | 1 1 1 1 1 1 1 1 1 1 | 2.00* | 6.99 | |
| 0.75 | 1 1 1 1 1 1 1 1 1 1 | 2.00* | 7.10 | |
| 12 | 0.999 | 1 1 1 1 1 1 1 1 1 1 2 | 2.00* | 6.91 |
| 0.99 | 1 1 1 1 1 1 1 1 1 1 2 | 2.00* | 7.16 | |
| 0.95 | 1 1 1 1 1 1 1 1 1 1 2 | 2.00* | 7.48 | |
| 0.90 | 1 1 1 1 1 1 1 1 1 1 2 | 2.00* | 7.65 | |
| 0.75 | 1 1 1 1 1 1 1 1 1 1 1 1 | 2.00* | 7.83 |
The gamma prior distribution on the number of virions places the specified coverage on the interval 4–400.
The marginal distribution of the observed data Y is a weighted average of binomial distributions
using (4) and (5).
A closed-form expression for this probability is given at (A2) in the Appendix along with the properties of this multivariate discrete distribution. The probabilities in Table I are calculated from the marginal distribution (6). Additional properties of this distribution appear in [20]. The sensitivity of the design to parameters α and σ of the prior distribution f given at (5) is discussed in Section 4.
A useful design criterion studied in [11] is to minimize the expected reciprocal information. That is, the design in n and the dilution rate dI are chosen as
where expectation is taken over the prior distribution.
Intuitively, such designs minimize the expected variance of . This objective was used to determine a dilution rate of dI =3.84 to illustrate our prototype design given in Table I. This prototype is compared with other designs n in Section 4. The design that minimizes (7) over all possible designs with 10 aliquots is given in Table III. Minimum expected reciprocal information designs are given in Table V for other small numbers of aliquots and other prior distributions on N. An alternative objective criterion for generating serial dilution designs is proposed next.
3. Maximum entropy design for k, d, and n
Statisticians facing the problem of designing a serial dilution study might speak in terms of the bias, variance, or efficiency of an estimator of N. The laboratory scientist, however, will often be contented with an estimate of N accurate only up to the nearest power of 10. The technician also seeks feedback that their work was performed accurately, without contamination or other laboratory artifact or error. The technician designing a serial dilution experiment has a loss function that is different from the one that the statistician has while designing a serial dilution motivated by other concerns. In this section we argue that the technician values information differently from the way a statistician does.
The technician wants a large number of outcomes that have reasonably large marginal probability of occurring. If only a few outcomes are likely to occur in practice then such a design would be viewed by the technician as requiring excessive aliquots and not providing sufficient feedback. The design in Table III, for example, offers only 10 different outcomes with probabilities greater than 0.005. In a dilution series with either a large sample size or else a prior distribution with a small variance it would be prudent to have all of the observations concentrated in such a manner that would minimize the variance of the estimate . This setting would favor the minimum expected reciprocal information design determined by (7).
In a small series without a strong prior distribution, each individual aliquot needs to serve both as confirmation of good laboratory practice as well as providing a unique amount of data by examining a different dilution level. Intuitively, in a small series lacking precise prior knowledge, the observations need to be spread out in order to locate the true number of virions N. This reasoning favors designs with many narrowly spaced dilutions and few replications at any one level. A small series also suggests that we avoid a design in which a few very high probability events are collectively expected to occur most of the time.
One reassurance of good practice in a design with a variety of different dilution levels is that there are few inconsistencies in which a low dilution detects virions but at the same time `skips' a higher concentration that fails to do so. A small number of these skips naturally appear with non-negligible probability in the designs of Tables I and III but are not of great concern because they skip only one dilution level. Intuitively, it would be of greater concern if the dilutions skipped two or more dilution levels but as we point out next, this is not always the case.
Skips of two levels are common and appear in Table IV. These outcomes are labeled with a. Skips of three levels also appear and two of these outcomes are labeled by b. Skips of two or more should be expected to occur almost 7 per cent of the time in this design. There are also staggered skipped levels in Table IV in which multiple skips are separated by detected levels. Two of these outcomes are labeled by c in this table.
The presence of large skips or unusual skipped patterns is more common than one might expect, so these alone are not necessarily indicative of contamination or poor laboratory practice. Nevertheless, these skips offer important feedback in dilution experiments with small sample sizes such as examined here.
One way to achieve such a small design with many levels is to avoid too many large marginal probabilities Pr[Y]. On a log-scale, the expected value
is also known as the entropy and measures the variability of Y.
Importance Of Serial Dilution Technique
Intuitively, the entropy (or randomness) is maximized when there are many possible outcomes and the probabilities of these are nearly equal in value. Designs that maximize the entropy will provide the technician with a large number of outcomes containing observations spread over a wide variety of dilutions k. Maximum entropy design is unique to small dilution series where there is frequently little a priori knowledge available and a number of feedback mechanisms are needed. In a larger series with many aliquots, there is greater opportunity to check the quality of the laboratory procedure and we would be able to concentrate on the precision of the estimate of initial virions N. In a small series such as examined here, there are other concerns that are of equal importance to the approximate variance of the estimate.
The maximum entropy design with 10 aliquots appears in Table IV. This design consists of k=10 stages and no replications at any stage, i.e. all ni=1. Only those outcomes with a marginal probability Pr[Y] greater than 0.005 are included. When we compare the designs of Tables III and andIV,IV, we see that the maximum entropy design provides many more high probability outcomes than the design that minimizes the expected reciprocal information, both with 10 total aliquots. The dilution rate dE is also determined by maximizing the entropy for the design specified in Table IV. This dilution rate is achieved at the boundary specified by (3).
4. More general applications
We return to the example of titration of virus inside syringes described in the Introduction that is limited to Σni=10 aliquots. Values of α=1.1168 and σ=9.8255×10−3 correspond to the gamma prior distribution (5) on N with 95 per cent coverage of the interval 4–400 and 2.5 per cent outside each end of this range. Other parameter values for the gamma prior distribution are discussed below and illustrated in Tables V and andVIVI.
Table II illustrates a variety of other possible designs, all with 10 aliquots. These were obtained by completely enumerating all possible designs with 10 aliquots and varying values of k and n. There are 512 possible combinations of designs for k=1,…,10 and all n=(n1,…,nk) taking non-zero values. Only those few designs with the smallest expected reciprocal information and greatest entropy are included in this table. Our prototype design of k=5 and n=(2,2,2,2,2) is included as a comparison.
Designs that minimize the expected reciprocal information tend to favor smaller values of k. In particular, of the six minimal expected reciprocal information designs listed in Table II all of these have k≤3 stages whereas smallest of this criterion has k=1. The details of this design appear in Table III. Of designs with k=2 or 3, these generally include most of the replications at the most dilute levels and smallest values of pi, where the data and information are the most difficult to collect.
Maximum entropy designs listed in Table II favor larger numbers of stages k, and of these, values of k=7,8, and 9 have the largest entropy among all designs with 10 aliquots. In these designs there is little opportunity for replicated aliquots and when these occur they tend to appear near the center and most dilute end of the series. Except for the design with k=10, the maximum entropy dilution rate dE is not greater than the dilution rate dI for the minimum expected information design. The design that maximizes the entropy over all possible designs with 10 aliquots is presented in Table IV. Out of Π(ni+1)=576 possible outcomes for this design, only those with a marginal probability Pr[Y]>0.005 are included.
We can demonstrate how the maximum entropy design spreads the region of interest across a wider range of values of N even though moments of are undefined. If we consider the conditional distribution of restricted to only those points where it is defined, then in the minimum expected reciprocal information design of Table III has expected value of 50.1 and standard deviation of 64.1. Similarly, in the maximum entropy design of Table IV has expected value of 144.5 and standard deviation of 169.7, restricting the distribution to those values for which it is defined.
Tables V and andVIVI illustrate the sensitivity of the proposed design to the specific choice of parameters of the gamma prior distribution. For serial dilution designs up to 12 aliquots we varied the coverage probability of the interval 4≤N≤400 of interest with equal probability in both of the tails outside this range. At 0.999 coverage, the gamma distribution concentrates on this interval and at 0.75 coverage, the gamma has longer tails that extend well beyond this interval. Intuitively, values of dI will increase with smaller prior coverage probabilities because the design needs to concentrate the data, all other things remaining equal. On the other hand, maximum entropy dilution rates dE generally decrease with lower prior coverage so as to spread the useful outcomes over a greater range of dilutions. The only example of an optimal minimum expected reciprocal information design with three aliquots occurs where the appropriate dilution rate is achieved at the boundary given by (3).
Tables V and andVIVI vary the number of aliquots for other small dilution series. For each number of aliquots given, only those designs with minimum expected reciprocal information and maximum entropy are listed. We are unable to generalize or prove mathematically, but the minimum expected reciprocal information designs tend to have small numbers of dilution levels k and all replicates appear at only one of these levels. The maximum entropy designs, on the other hand, all have large numbers of dilution levels (except at 4 aliquots) and few replicates located near the center or most dilute end of the series.
Acknowledgments
Contract/grant sponsor: Yale Center for Interdisciplinary Research in AIDS; contract/grant number: MH62294
Appendix A: The marginal distribution of Y
In this Appendix we derive the marginal distribution of Y. Additional details about this occupancy distribution are discussed in [20].
Conditional on N,the Y={Yi} are jointly distributed as independent binomial random variables with respective parameters n={ni} and pi(N) given at (1). A gamma prior distribution with density function (5) is assumed for the number of viral particles N>0 in the original solution for parameters α>0 and σ>0.
Define
so that θi>0 and pi=1−exp(−Nθi) with {λi} defined at (2). This re-parameterization in θ={θi} will simplify the notation that follows.
The marginal distribution of the aliquot outcomes Y is a weighted average of binomial distributions
where
The integral can also be written in closed form. We first write
so that marginally,
Importance Of Serial Dilution In Serology
This distribution is among the family of occupancy distributions describing the distribution of the number of urns containing at least one ball, or in our case, vials containing at least one viral particle [21]. The univariate distribution of each Yi is expressible as the sum of ni exchangeable Bernoulli random variables and follows the general form given in [22].
The posterior mean of N satisfies
Serial Dilution
All of the θi in (A2) can be re-scaled so without loss of generality we can assume that σ=1 in the remainder of this Appendix. The moments of the multivariate distribution at (A2) can be described as follows.
In particular,
and
For i≠j, Yi and Yj are conditionally independent given N. The marginal covariance between Yi and Yj in (A2) is
All of these covariances are non-negative.